« Que l’homme contemple donc la nature entière dans sa haute et pleine majesté (…), que la terre lui paraisse comme un point au prix du vaste tour que cet astre décrit et qu’il s’étonne de ce que ce vaste tour lui-même n’est qu’une pointe très délicate à l’égard de celui que les astres qui roulent dans le firmament embrassent. Mais si notre vue s’arrête là, que l’imagination passe outre; elle se lassera plutôt de concevoir, que la nature de fournir. Tout ce monde visible n’est qu’un trait imperceptible dans l’ample sein de la nature. Nulle idée n’en approche. Nous avons beau enfler nos conceptions au-delà des espaces imaginables, nous n’enfantons que des atomes, au prix de la réalité des choses. C’est une sphère dont le centre est partout, la circonférence nulle part.(…)
Mais pour lui présenter un autre prodige aussi étonnant, qu’il recherche dans ce qu’il connaît les choses les plus délicates. Qu’un ciron lui offre dans la petitesse de son corps des parties incomparablement plus petites, des jambes avec des jointures, des veines dans ces jambes, du sang dans ces veines, des humeurs dans ce sang, des gouttes dans ces humeurs, des vapeurs dans ces gouttes; que, divisant encore ces dernières choses, il épuise ses forces en ces conceptions, et que le dernier objet où il peut arriver soit maintenant celui de notre discours; il pensera peut-être que c’est là l’extrême petitesse de la nature. Je veux lui faire voir là dedans un abîme nouveau. Je lui veux peindre non seulement l’univers visible, mais l’immensité qu’on peut concevoir de la nature, dans l’enceinte de ce raccourci d’atome. Qu’il y voie une infinité d’univers, dont chacun a son firmament, ses planètes, sa terre, en la même proportion que le monde visible; dans cette terre, des animaux, et enfin des cirons, dans lesquels il retrouvera ce que les premiers ont donné; et trouvant encore dans les autres la même chose sans fin et sans repos, qu’il se perde dans ses merveilles, aussi étonnantes dans leur petitesse que les autres par leur étendue »
Les pensées de Pascal
Pour démarrer, une première remarque : Ni Nico ni moi ne sommes les premiers à être tatillons sur l’usage du mot « infini » hors contexte mathématique. Pour preuve ce texte hyper connu de Pascalsur les deux infinis, ou encore Archimède lui-même : histoire de montrer à tout le monde qu’il n’y avait pas d’infini dans ce bas monde, il a fait une estimation (haute), du nombre de grains de sable que l’on pourrait caser dans l’univers. Bon, évidemment, on ne ferait plus le calcul comme lui en mettant la terre au centre d’une sphère où sont collées les étoiles. Mais l’idée est là : il y a des nombres gigantesques, des tailles minuscules, sans que tout cela ait un rapport quelconque avec l’infini. Un grain de sable, un atome, ou n’importe quel objet physique a une certaine taille. Il est donc bien impossible d’en mettre une infinité dans un espace fini, même très grand.
 |
| Beaucoup de grains de sables très petits. |
À l’inverse, sur un segment, objet fini, on case… une infinité de points ! Si vous n’en êtes pas convaincus, deux petites questions :
Qu’obtient-on quand on coupe un segment en deux ? En principe, deux segments, plus petits.
Pouvez-vous imaginer un segment que l’on ne peut pas couper en deux ? À l’inverse de la dernière part de gâteau que tout le monde coupe et recoupe en deux pour ne pas être celui qui finit, et qui termine en miette que l’on ne coupera pas, un segment si petit soit-il peut toujours être coupé en deux. Là encore, si vous êtes dubitatifs (et ce n’est pas cochon), il est relativement simple de se convaincre : un segment, c’est une certaine longueur, donc un certain nombre qui ne vaut pas 0. Et on peut toujours diviser un nombre par deux, s’il n’est pas nul, on ne tombera pas sur zéro, mais sur un nombre positif : la longueur des deux segments obtenus.

On peut toujours couper un segment en deux, et le résultat aussi… Il y a bien une infinité de points sur le segment AB
Résumons : on peut toujours couper un segment en deux ; le résultat est deux segments. Que l’on peut donc à nouveau couper en deux. Et il n’y a pas de raison que ça s’arrête. Or chaque coupe est faite sur un point. Il y a donc bien une infinité de points sur un segment, qui est pourtant d’une longueur finie. Syncope chez les physiciens.
 |
| Physicien découvrant un segment mathématique |
Il est temps de ressortir le vieux Zénon : on oublie souvent qu’il n’a pas qu’un paradoxe à son arc… Le plus connu, raconté avec Achille et la tortue, ou avec une pierre qu’on jette vers un mur, s’oppose à cette vision continuiste du monde : si on peut toujours couper en deux une durée ou un espace, alors Achille ne rattrapera jamais la tortue, une pierre lancée contre un mur ne l’atteindra jamais (elle ne quittera même jamais la main de la personne qui la lance) car il faut passer par une infinité d’étapes (voir l’illustration plus haut de l’infinité de points sur un segment)
D’autres paradoxes s’opposaient à la vision concurrente proposée à l’époque : l’« atomisme ». Certains penseurs grecs pensaient en effet que le monde était fait d’atomes, pas au sens actuel, mais au sens de « plus petit élément », que l’on ne peut pas casser, et avec du vide entre eux.
Contre la vision atomiste, Zénon propose entre autres le paradoxe de la flèche : si le temps est constitué d’atomes, alors on peut considérer la flèche à un instant donné. Or à un instant donné, la flèche est immobile, à un endroit précis. Sa vitesse est donc nulle. Elle ne peut donc pas bouger…
Il faut bien dire qu’effectivement, réussir à donner un sens à la notion de « vitesse instantanée » est bien délicat. En gros, on voudrait dire que c’est un instant « un peu épais », ou un intervalle de temps vraiment très très court.
On ne sort pas de là : si on ne peut pas couper un infiniment petit, c’est un point. Sinon, il a une certaine taille, et n’a donc rien d’infiniment petit.
La notion de « point » en géométrie classique fait le premier choix : un tel point n’a donc pas de largeur, pas de longueur, pas d’épaisseur. La définition proposée par Euclide reprend bien les termes du problème : « un point est ce qui n’a pas de partie », autrement dit ce qu’on ne peut pas couper en deux. L’une des conséquence les plus fâcheuses pour l’intuition est sans doute qu’il y a autant de points sur deux segments de taille différente, et même sur une droite. Il est relativement simple de s’en convaincre, par exemple pour deux segments : placez les parallèlement, l’un au dessus de l’autre.
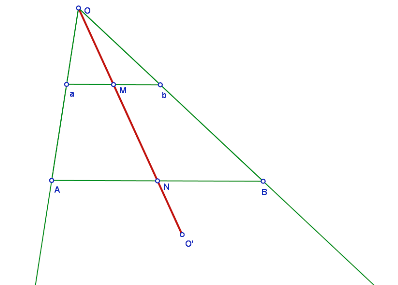
On relie a à A et b à B, et on obtient O. Toute demi-droite partant de O indique à tout point du segment du haut, (ici M) à qui il doit serrer la main en bas (ici N) et réciproquement. Il y a donc autant de monde en haut et en bas…
Reliez les extrémités les unes aux autres. Le point obtenu permet d’« envoyer » chaque point de l’un des segment sur l’autre, et vice versa. On a donc une correspondance entre chaque point de l’un des segments et chaque point de l’autre. Comme si chaque point de l’un serrait la main d’un point de l’autre. Et pourtant, il n’y a pas de points plus tassés d’un côté que de l’autre, ni de point plus gros ou plus petit… Arrangez-vous avec ça.
On peut reprendre la perplexité de d’Alembert :
« Une quantité est quelque chose ou rien (…). L’idée qu’il puisse y avoir un état intermédiaire entre ces deux est une chimère »
Leibniz, lui, ne semble pas plus perturbé que ça, même s’il n’est pas très très clair :
« Je juge d’ailleurs que deux termes sont égaux non seulement lorsque leur différence est absolument nulle, mais aussi lorsqu’elle est incomparablement petite, et bien qu’on ne puisse dire en ce cas que cette différence soit absolument Rien, elle n’est pourtant pas une quantité comparable à celles dont elle est la différence. Ajoutons à une ligne un point d’une autre ligne, ou une ligne à une surface, nous n’accroissons pas leur grandeur. Il en va de même si nous ajoutons à une ligne une autre ligne mais incomparablement plus petite. Aucune construction ne peut montrer non plus un tel accroissement. »
Bon bon bon… C’est limpide, c’est un truc vraiment très petit
Mais pourquoi donc s’acharner sur ces objets qui sont si malaisé à appréhender ? Parce qu’on en a besoin, au moins pour l’intuition, notamment en math et en physique.
Premier exemple : les formes courbes. Comment donner un sens à une longueur, une surface ou un volume courbe ? A priori, ce que l’on sait faire sans réfléchir, c’est calculer des longueurs droites (le théorème de Thalès et celui de Pythagore par exemple le permettent dans bien des situations), des surfaces de polygones (tout polygone peut se découper en petits triangles, et on sait calculer la surface d’un triangle), mais dès qu’il y a courbe, à commencer bien sûr par le cercle, c’est la panique : on ne sait pas faire. (et ce problème a d’ailleurs occupé et continue d’occuper, d’une manière ou d’une autre, une bonne partie des mathématiciens, mais pas pour le cercle, quand même !)
Pourtant, en réfléchissant deux minutes, on se rend bien compte qu’une courbe, c’est un peu comme plein de toute petites lignes droites (nous parlons là de courbes « gentilles », pas d’horreurs comme les fractales). Nico a par exemple bien décrit, dans son dossier, la méthode utilisée parArchimède pour calculer le périmètre d’un cercle : il calcule le périmètre de polygones extérieurs et intérieurs au cercles ; plus ces polygones ont des côtés petits, plus ils se rapprochent du cercle.
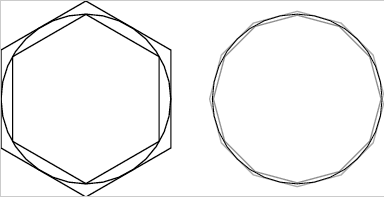
La méthode d’Archimède : on coince un truc rond entre deux suites de polygones. Et on évite bien de dire qu’on continue jusqu’à ce que les côtés soient « infiniment petits »…
Un grec de l’Antiquité aurait certainement hurlé en entendant cette phrase, mais en gros on « sent » qu’un cercle, c’est un polygone avec une infinité de côté infiniment petits. Oui mais bon, on a vu que ça ne voulait pas dire grand chose…
Les physiciens, quant à eux, auraient bien envie de savoir ce que veut dire une vitesse instantanée, par exemple. Une vitesse moyenne, on voit bien : on prend la distance parcourue pendant un certain temps, par exemple 30 mètres en dix secondes, et on dit que la flèche s’est déplacée à une vitesse moyenne de 3 mètres par seconde. Mais elle ne va pas toujours à la même vitesse. Et dans bien des situations, les physiciens seraient content de pouvoir dire : « à cet instant, la flèche va à telle vitesse ».
Pour s’en sortir, on peut botter en touche. Voilà un petit florilège d’évitements des infiniment petits :

Un infiniment petit ? Où ça ?
Pour démontrer qu’une surface a telle grandeur, Archimède la coince donc entre deux suites de polygones dont on sait calculer les surfaces. et pour lesquels on démontre que la différence entre les deux surfaces peut être rendue plus petite que n’importe quel nombre donné ; on passe ensuite par un raisonnement par l’absurde pour conclure : la surface qui nous intéresse ne peut pas être plus grande que l’un des polygones plus grand, ou plus petite que l’un des plus petits. Donc elle vaut bien la valeur que l’on attend. Ouf !
L’idée de la théorie de l’intégration, datant du 19ème siècle, est à peu près la même, juste mise en forme rigoureuse. Elle permet de calculer de façon bien plus efficace et dans des situations bien plus variées des objets courbes. L’idée principale est celle de limite : on approche une courbe avec des rectangles, en faisant donc des « escaliers ». Puis on « fait tendre » la taille des marches vers 0. jamais on ne parle donc d’un infiniment petit. Pour ce qui est de la vitesse instantanée, c’est la limite de la vitesse moyenne quand l’intervalle de temps tend vers 0… On s’en sort donc avec des points et des limites, pas d’infiniment petit en vue.
Entre deux, au XVIIe siècle, Cavalieri, lui, est parti d’une vision plus intuitive : il paraît naturel de dire qu’un volume est un empilement de plans, une surface un empilement de lignes, et une ligne une succession de points. Et en même temps, c’est gênant, puisque si un point n’a pas de dimension, on n’obtiendra jamais un segment même en en mettant une infinité. De même, on n’obtiendra jamais une surface en empilant des lignes qui n’ont pas de largeur, ou un volume avec des surfaces sans épaisseur.
Mais Cavalieri sait rester prudent : Tout ce qu’il dit, c’est que si deux surfaces sont prises entre deux droites parallèles, et qu’à toute « hauteur » choisie, les deux « tranches » obtenues dans les deux surfaces sont de même longueur (ou toujours dans le même rapport), alors ces deux surfaces sont égales (ou on déduit l’une de l’autre par une règle de trois). Cette méthode fonctionne bien entendu également avec des volumes coincés entre deux plans parallèles. Pour prendre une image peut-être plus concrète, prenez deux paquets de cartes identiques, et posez les côte à côte sur une table. Donnez aux paquets la forme que vous le voulez, en laissant bien les cartes empilées l’une sur l’autre (vous pouvez faire des »vagues » sur le côté, une spirale comme les pros du poker ou les magiciens…). En coupant par des plans horizontaux, vous rencontrerez dans chaque paquet, à chaque hauteur, une même surface : celle d’une carte. Cela nous assure, dit Cavalieri, que ces deux paquets ont un même volume.
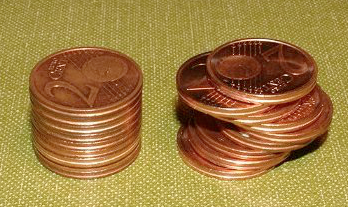
ici, l’idée avec des pièces : le « cylindre » de gauche a le même volume que le truc tarabiscoté de droite.
Pour un exemple détaillé de la méthode de Cavalieri :
http://www.palais-decouverte.fr/fileadmin/fichiers/infos_sciences/mathematiques/textes/formes_matematiques_revue/355_mar_avr_2k8.pdf
et un autre là
http://www.palais-decouverte.fr/fileadmin/fichiers/infos_sciences/mathematiques/textes/formes_matematiques_revue/356_mai_juin_2k8.pdf)
Évidemment, ça ne marche pas avec des cartes ou des pièces, puisqu’il y a des « marches » à chaque étage.
Cette méthode, quoi qu’efficace, a été très critiquée. Notamment parce qu’on ne sait pas bien ce que sont ces indivisibles… additionnant des lignes, on obtient une surface, et en additionnant des surfaces, on obtient des lignes. Certains tenant de la méthode se sont défendus : il ne s’agit pas vraiment de lignes, mais de rectangles très très fins. On y revient… Sauf que s’il s’agit réellement de rectangles, alors ça ne marche pas.
Autre critique : pourquoi ça ne marche que quand les « indivisibles » sont parallèles ? Dans d’autres cas, les contre exemples foisonnent.
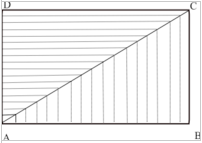
Exemple d’indivisibles qui tournent mal : il semblerait qu’il y en a autant horizontaux et verticaux. Il est clair que les horizontaux sont plus longs que les verticaux. Donc le triangle ACD devrait être plus grand que ABC. Or il a également la même surface ! Où est l’arnaque ?
Râclements de gorges chez les tenants des indivisibles : « Oui non mais… En fait, il y a des indivisibles « plus gros » que d’autres… »
Bon, en gros, la méthode a l’air de marcher, mais elle demande d’admettre des indivisibles dont personne ne sait vraiment ce qu’ils sont.
Passons maintenant à ceux qui osent se lancer :
Pascal ou Roberval, par exemple, soutiennent les indivisibles, considèrent qu’ils ont une véritable existence.
Pascal :
« Et c’est pourquoi je ne ferai aucune difficulté dans la suite d’user de ce langage des indivisibles, la somme des lignes ou la somme des plans (…) [ceux] qui s’imaginent que c’est pécher contre la géométrie que d’exprimer un plan par un nombre indéfini de lignes ; ce qui ne vient que de leur manque d’intelligence, puisqu’on n’entend autre chose par là sinon la somme d’un nombre indéfini de rectangles faits de chaque ordonnée avec chacune des petites portions égales (…), dont la somme est certainement un plan, qui ne diffère de l’espace [recherché](…) que d’une quantité moindre qu’aucune donnée. »
Roberval va lui jusqu’à dire que les indivisibles existent dans le monde réel, ce qui lui vaudra quelques problèmes avec la religion… On ne contredit pas Aristote comme ça. Pour lui en tous cas, les indivisibles d’une surface sont forcément des surfaces : il y a sinon un problème d’« homogénéité ». De même qu’on n’obtient pas des carottes en additionnant des choux, on ne peut pas obtenir une surface en additionnant des longueurs. (Petite parenthèse histoire de se perturber un peu : l’avenir dira que c’est un peu plus compliqué que ça, puisque Peano a trouvé début XXe siècle une courbe (certes de longueur infinie) qui rempli littéralement un carré… Pourtant la ligne est « infiniment fine », elle n’a pas de largeur !)
Bref, c’est un peu foutraque.
Un peu plus tard, les débuts du « calcul infinitésimal » va reprendre cette idée de façon beaucoup plus barbare encore. Newton et Leibniz sont les deux « inventeurs » de cette méthode permettant de résoudre des problèmes posés depuis l’Antiquité.
En gros, ils introduisent la notion de « dx », qui signifie intuitivement « juste après » ou « presque rien ». Or le point ou l’instant d’après, je ne vous apprend plus rien, ça ne veut rien dire, bien sûr. On ne peut voir le continu comme une série d’instants… Mais la méthode marche, et permet notamment de donner un sens à « vitesse instantanée ». Et ça, quand une méthode marche… Il n’y a généralement plus personne pour la rejeter.
Mais quand même, cette époque est hallucinante : On fait absolument n’importe quoi, on divise des infinitésimaux par des infinitésimaux, et on donne un résultat (ce qui revient à donner un résultat à 0/0 !?!?) On décrète que les infinitésimaux ne sont pas tous de la même nature, que certains sont négligeables par rapport à d’autres…
Revenons à Leibniz, pour la suite de l’explication limpide vue plus haut :
« Je considère que seules sont comparables des grandeurs homogènes, dont le produit de l’une par un nombre, un nombre fini s’entend, peut surpasser l’autre. Je pose donc que des grandeurs dont la différence n’est pas de cette nature sont égales, comme l’admit également Archimède et tout le monde après lui. C’est précisément dans ce cas qu’on dit qu’une différence est plus petite que toute grandeur donnée. Le procédé d’Archimède permet toujours de le confirmer au moyen d’un raisonnement par l’absurde. Toutefois, comme la méthode directe est plus immédiatement compréhensible et plus expédiente pour inventer, il suffit, une fois qu’on a compris cette démonstration régressive, d’appliquer la méthode directe consistant à négliger les quantités incomparablement plus petites, méthode qui porte en elle-même sa propre justification conformément aux lemmes que j’ai publiés en févier 1689. Rejeter pareille définition de l’égalité, c’est faire une querelle de mots. »
L’idée de base est exactement la même que depuis l’Antiquité, sauf qu’on se permet d’écrire directement que l’on fait la somme de tous les infinitésimaux. Fini les précautions de toute sortes. Les Grecs de l’Antiquité auraient déjà eu du mal à accepter qu’on puisse faire une somme avec une infinité de terme (comme la fameuse somme 1 + ½ + 1/4 + 1/8 + 1/16 + … qui vaut 2, pour résoudre l’un des paradoxe de Zénon), mais là on fait carrément une somme sur tous les points d’un segment, voire d’une droite, bref, sur un truc continu !
On trouve un élément essentiel dans ce texte, qui commence à donner une idée de propriété de ce que sont les infiniment petits : si on veut qu’ils soient tels que nous les voulons, il faut que, multipliés par n’importe quel nombre, ils restent plus petits que n’importe quel nombre. Cela s’oppose à un axiome sur les nombres, proposé par Eudoxe dans l’Antiquité : si on prend deux nombres quelconques, A et B, A plus petit B. Alors il existe un nombre n tel que n x A est plus grand que B. S’il avait trouvé nécessaire de le donner, c’est qu’il sentait bien que ce n’était pas forcément évident… à cause de notre intuition des infiniment petits.
Pour les plus attentifs du podcast, particulièrement attentifs aux maths, vous devez vous souvenir d’une note d’El jj lue par Nico ici présentant une construction de nombres « surréels » qui ne vérifiaient effectivement pas cet axiome. Plusieurs constructions rigoureuses de ce type existent, l’une des plus connues étant l’« analyse non standard », qui a pris son essor dans les années 60. L’idée est toujours la même : rajouter des nombres aux nombres réels.
Pour résumer, il existe donc des nombres « standards », ceux auxquels nous sommes plus ou moins habitués. Et puis, on définit (proprement, ce n’est pas si simple, je ne rentre pas dans les détails) des nombres qui sont plus grands que n’importe quel nombre standard : des infiniment grands. Il y en a bien sûr une infinité. Et il y a toujours un nombre infiniment grand plus petit qu’un nombre infiniment grand donné, on peut imaginer une suite infinie de nombres infiniment grands de plus en plus petits tous plus grand que tous les nombres « standards ». Arrangez-vous avec ça.
Évidemment, à l’autre bout, il y a les infiniment petits, (enfin !) ceux qui sont plus proches de 0 que n’importe quel nombre standard. L’inverse d’un infiniment grand est bien entendu un infiniment petit, et vice versa. Notez que l’on n’est toujours pas capable de donner un sens à des expressions comme : « le point juste après un autre ». Il y a toujours une infinité de points entre deux points… Et les points sont toujours aussi tassés sur un segment.
Pour voir les choses de façon géométrique, le résultat est une droite couverte de « halos » plutôt que de points : un halo est un nombre réel standard, et tous les nombres qui lui sont infiniment proche, soit ce nombre plus ou moins un nombre infiniment petit. Un exemple : 0,3333…333, pour peu que l’on ai mis un nombre infiniment grand de 3, est infiniment proche de 1/3 et fait donc partie de son « halo ».
Il n’est pas sûr que ce monde soit beaucoup plus intuitif que l’autre, surtout quand on n’y est pas habitué ! Reste qu’effectivement, on dispose enfin d’infiniment petits. Certaines choses s’écrivent alors de façon beaucoup plus simple. Prenons un exemple bête : la continuité. Intuitivement, une courbe est continue si on peut la tracer d’un coup de crayon sans interruption. Une petite « histoire pour tenter d’expliquer un peu mieux le changement de formulation que permettent les infiniment petits :
Un marcheur part à 8h de chez lui, et arrive dans la ville voisine à 12h. Il peut à tout moment s’arrêter, faire demi-tour, accélérer… Savoir si son trajet est continu revient simplement à savoir s’il existe un moment où il s’est téléporté ou non. La façon de voir « classique » est de dire : si son trajet est continu à 10h (c’est à dire qu’il ne s’est pas téléporté à 10h), alors quelle que soit la distance que vous m’imposez, je peux trouver un intervalle de temps pendant lequel il n’était pas plus loin que cette distance du point où il se trouvait à 10h.
La version « Analyse non Standard » : pour tout instant infiniment proche de 10h, il était infiniment proche du lieu où il se trouvait à 10h.
Les deux façons de faire sont rigoureusement équivalentes, la seule différence est qu’on n’utilise pas les mêmes outils pour décrire une même propriété.
Les tenants de l’ANS disent que c’est plus intuitif, que les physiciens réfléchissent tous comme ça, et que c’est donc une bonne idée de leur fournir un tel outil, qui permettra de trouver de nouveaux résultats.
Les opposants disent que certes ça fonctionne, mais que ça n’apporte rien de nouveau. Donc à quoi bon
Certains vont même plus loin, et proposent donc d’autres modèles qui conviendraient mieux aux physiciens contemporains, qui ne s’occupent plus tellement de mécanique élémentaire, mais plutôt de physique quantique ou de trucs comme ça, où les choses se passent encore très différemment. J’avoue que je me sens assez incompétent pour prendre position !
Pour terminer, d’autres notions qui peuvent d’une manière ou d’une autre évoquer une forme « d’infiniment petit » :
La notion de « négligeable », par exemple, est bien utile dans et hors des maths. On arrive à justifier rigoureusement que certaines quantités sont tellement petites qu’on a le droit de les négliger quand les conditions sont réunies. Ce qui permet par exemple de dire que quand l’angle est petit, le sinus de cet angle vaut presque la même chose que la valeur de cet angle, avec la bonne unité.
La notion de « mesure » permet également de parler d’objets infiniment petits. En gros, on a mis au point des méthode permettant de mesurer un ensemble de points. Prenons le cas le plus simple : dans le cas d’un segment, sa mesure vaudra sa longueur. La mesure d’un point vaudra donc 0. Mais également la mesure de deux points, de trois, de… Jusqu’à combien ? En fait, on sait qu’il existe des ensemble de points « aussi gros » que l’ensemble des points de toute la droite qui ont une mesure de …0. Ce qui signifie qu’il n’y a pas que la quantité qui compte, l’essentiel est dans l’arrangement des points… Et qu’on peut considérer comme infiniment petit un ensemble très gros ! (sur des ensembles de mesure nulle, voir mon dossier sur le hasard)
On 29.09.2013 by Robin
http://www.podcastscience.fm/dossiers/2013/09/29/linfiniment-petit/

Aucun commentaire:
Enregistrer un commentaire